Example f (x) = 2x3 and g (x) = x2 "x" is just a placeholder To avoid confusion let's just call it "input" f (input) = 2 (input)3 g (input) = (input)2 Let's start (g º f) (x) = g (f (x)) First we apply f, then apply g to that result (g º f) (x) = (2x3) 2 The first derivative of a function See calculus In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);

The Agony And Dx Dt The Meaning Of F X
F(x)=1/x mean value theorem
F(x)=1/x mean value theorem- 1 #define square (X) (x* (x)) is a macro, therefore the compiler replaces the macro with the code square (x3) = x3* (x3) = 53* (53) = 53* (8) = 29 Share Improve this answer edited Feb 2 '13 at 1439 leemesX x variable unknown value to find when 2x = 4, then x = 2 ≡ equivalence identical to ≜ equal by definition equal by definition




Solving Trigonometric Equations Concept Methods
// some more code return x;Modifier modifier le code modifier Wikidata En mathématiques , la fonction exponentielle est la fonction notée exp qui est égale à sa propre dérivée et prend la valeur 1 en 0 Elle est utilisée pour modéliser des phénomènes dans lesquels une différence constante sur la variable conduit à un rapport constant sur les images Ces phénomènes sont en croissance diteA derivative is a function which measures the slope It depends upon x in some way, and is found by differentiating a function of the form y = f (x) When x is substituted into the derivative, the result is the slope of the original function y = f (x)
I find it helps sometimes to think of a function as a machine, one where you give a number as input to the machine and receive a number as the output The name of the function is the input is x and the output is f (x), read " f of x" The output f (x) is sometimes given anSymbol Symbol Name Meaning / definition Example;The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable x It is called the derivative of f with respect to x If x and y are real numbers, and if the graph of f is plotted against x, derivative is the slope of this graph at each point
All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction Square 3 Square −3 Definition 86 Total Differential Let \(z=f(x,y)\) be continuous on an open set \(S\) Let \(dx\) and \(dy\) represent changes in \(x\) and \(y\), respectivelyComposing Functions at Points Suppose you are given the two functions f ( x) = 2 x 3 and g ( x) = – x2 5 Composition means that you can plug g ( x) into f ( x) This is written as " ( f o g ) ( x) ", which is pronounced as " f compose g of x " And " ( f o g ) ( x) " means " f ( g ( x) )"




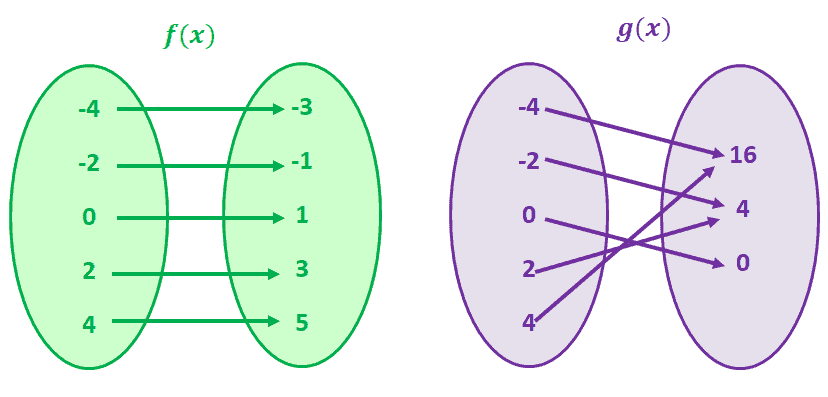
Each Element In A Must Be Matched With An Element In B Ex 0 3 3 2 9 4 12 5 Some Elements In The Range May Not Be Matched With The Domain Two Ppt Download



Limit Definition Of A Derivative
Replace f(x) by y if necessary;Explanation In the relation , there are many values of that can be paired with more than one value of for example, To demonstrate that is a function of in the other examples, we solve each for can be rewritten as can be rewritten as can be rewritten as need not be rewritten For the function f (x) = xn, n should not equal 0, for reasons which will become clear n should also be an integer or a rational number (ie a fraction) The rule is f (x) = xn ⇒ f '(x) = nxn−1 In other words, we "borrow" the power of x and make it the coefficient of the derivative, and then subtract 1 from the power




Limits



Increasing And Decreasing Functions
F 1 (x) is the standard notation for the inverse of f (x) The inverse is said to exist if and only there is a function f 1 with ff 1 (x) = f 1 f (x) = x Note that the graph of f 1 will be the reflection of f in the line y = x This video explains more about the inverse of a functionDisclaimer All content on this website, including dictionary, thesaurus, literature, geography, and other reference data is for informational purposes onlyThe abbreviation f(x) (French) means "fon Here's a list of examples and english translations for f(x)




2 5 1 Explain The Meaning Of Lim F X 10 Choose The Chegg Com



Fx Meaning Text Forex Winner Robot
Replace y with f1 (x) if the inverse is also a function, otherwise leave it as y; What's the definition of Fx and Fx, where F is a field?Let f(x)ℝ→ℝ be a realvalued function y=f(x) of a realvalued argument x (This means both the input and output are numbers) Graphic meaning The function f is a surjection if every horizontal line intersects the graph of f in at least one point Analytic meaning The function f is a surjection if for every real number y o we can find



Www3 Nd Edu Apilking Math Calc1lectures Lecture 3 limits Pdf




How Do You Find F X Using The Definition Of A Derivative For F X 4 X 1 4x Socratic
Example 4 The function f(x) = x 2 / (x 2 1), x≥0 The restriction is important to make it 11 Start with the function f(x) = x 2 / (x 2 1Let f (x) f(x) f (x) be a function defined on an open interval around x 0 x_0 x 0 (f (x 0) \big(f(x_0) (f (x 0 ) need not be defined) \big) We say that the limit of f ( x ) f(x) f ( x ) as x x x approaches x 0 x_0 x 0 is L L L , ieDefinition of Convexity of a Function Consider a function y = f (x), which is assumed to be continuous on the interval a,b The function y = f (x) is called convex downward (or concave upward) if for any two points x1 and x2 in a,b, the following inequality holds f ( x1 x2 2) ≤ f (x1) f (x2) 2 If this inequality is strict for any x1




How Do You Find F 3 Using The Limit Definition Given F X X 2 5x 3 Socratic




Chapter 4 Applications Of Derivatives 1 4 1
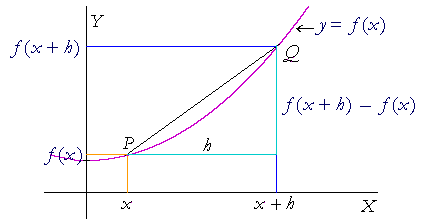
Which means f '(a) = 2a What about the derivative of f(x) = x nSimilar calculations, using the binomial expansion for (xy) n (Pascal's Triangle), yieldF ( x h) − f ( x) in such a way that we can divide it by h To sum up The derivative is a function a rule that assigns to each value of x the slope of the tangent line at the point ( x, f ( x )) on the graph of f ( x ) It is the rate of change of f ( x) at that pointWe set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x



Users Math Msu Edu Users Magyarp Math133 6 7 Hyperbolic Fcns Pdf



Graphs Of Functions
Decide whether $f(x)=x$ is bounded above or below on the interval $0,a$ where $a$ is arbitrary, and whether the function takes on it's maximum or minimum value within that same interval This question is very straightforward, assuming $x=x$ But if that is the case, then the choice of notation is very strangeF/X Also found in Dictionary, Financial, Encyclopedia, Wikipedia Acronym Definition F/X Effects F/X Foreign ExchangeHow to find the composite functions fog(x) and gof(x)A composite function can be thought of as a result of a mathematical operation that takes two initial fu



What Does F X X Mean Quora



Renethajb Files Wordpress Com 19 09 1 Function Dcs Part 3 Discrete Module 1 Cs 1 Pdf
The expression "f (x)" means "a formula, named f, has x as its input variable" It does not mean "multiply f and x "!F (x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domain However, range is sometimes used as a synonym of codomain, generally in old textbooksShow that f is differentiable at x=1, ie, use the limit definition of the derivative to compute f'(1) Click HERE to see a detailed solution to problem 9 PROBLEM 10 Assume that Show that f is differentiable at x=0, ie, use the limit definition of the derivative to compute f'(0) Click HERE to see a detailed solution to problem 10




Explain The Meaning Of The Following Equation Chegg Com



Optimization Theory
I'm looking for the meaning of "f(x)"?A zombie face emoticon The f's represent handsIf F(x)=x has no real solution then also F(F(x)=x has no real solution



What Does F 1 X Mean Quora



What Is The Meaning Of A Small O In Between Function Names I E F O G Mathematics Stack Exchange
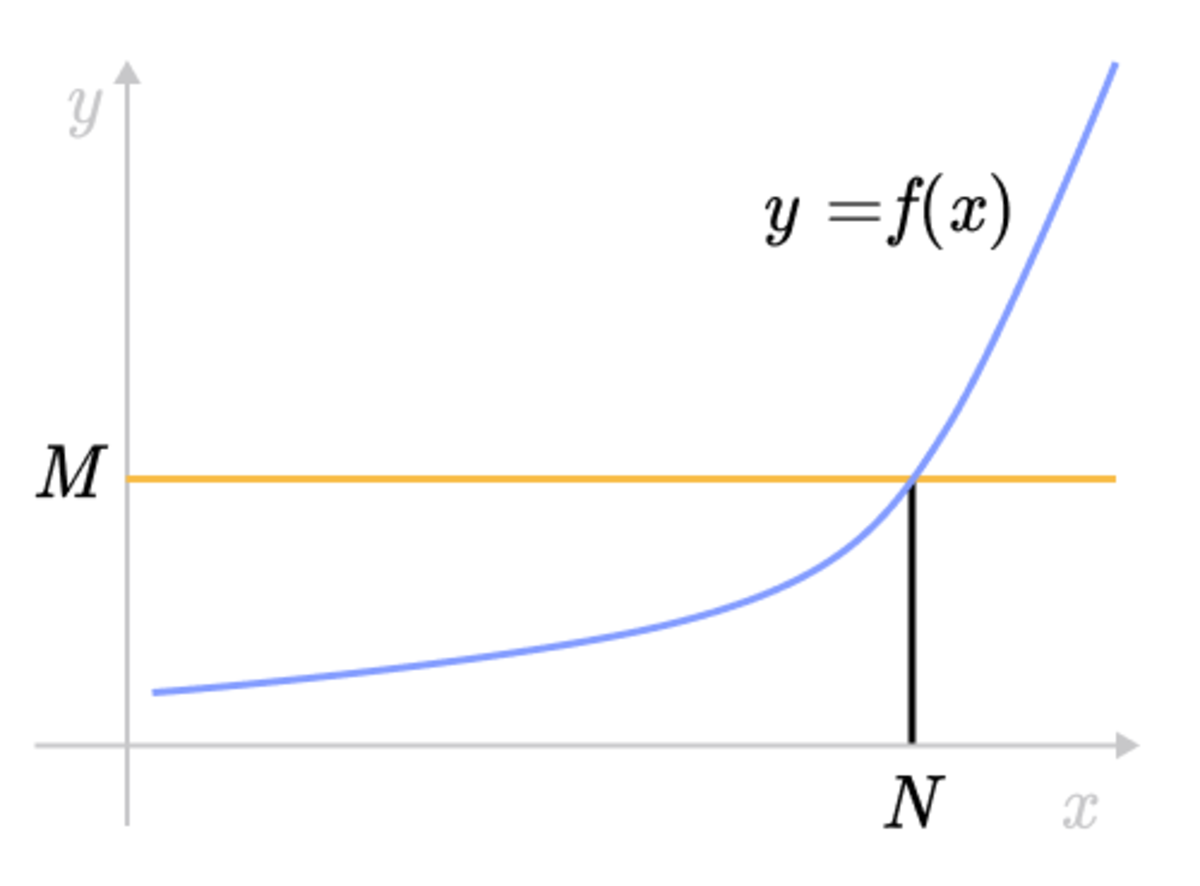
Derivative definition The derivative of a function is the ratio of the difference of function value f (x) at points xΔx and x with Δx, when Δx is infinitesimally small The derivative is the function slope or slope of the tangent line at point xSimply put, the Y=f(x) equation calculates the dependent output of a process given different inputsGiven a function f (x) f(x) f (x) and a real number a, a, a, we say lim x → a f (x) = ∞ \lim_{x\to a} f(x) = \infty x → a lim f (x) = ∞ If the function can be made arbitrarily large by moving x x x sufficiently close to a, a, a,



Answered Let F X 7 Sin X F X Is Less Bartleby



Q Tbn And9gcqnye10zfu7n1e5psc 7oyuuimkr8sjknkcqpbj1hdnr3gsgvai Usqp Cau
Use the definition to find the derivative of f (x) = a x^2 bx c Solution to Example 2 We first find difference quotient \dfrac {f (xh)f (x)} {h} = \dfrac {a (x h)^2 b (x h) c ( a x^2 b x c )} {h} Expand the expressions in the numerator and group like terms = \dfrac {a x^2 2 a x h a h^2 b x b h c a x^2 b xF (x) basically means y, and f' (x) means dy/dx The x can have a value, so for example, f (x) = 2x 1, then f (1) = 3 that is as good as I can explain it!!!} In main you can use like



The Meaning Of The Derivative An Approach To Calculus



One To One Function Explanation Examples
Définition formelle Soit {;} Soient f et g deux fonctions de la variable réelle xOn suppose que g ne s'annule pas sur un voisinage de aOn dit que f est équivalente à g en a, ou que g équivaut à f en a, et on note → (), lorsque () = → (())Exemple → Domination La notation grand O de Landau dénote le caractère dominé d'une fonction par rapport à une autreDefinition Sei eine Menge und → eine FunktionDann heißt ein Punkt Fixpunkt, falls er die Gleichung = erfüllt Anmerkungen Ist → eine lineare Abbildung auf dem Vektorraum, dann nennt man die Fixpunkte von auch FixvektorenDa jede lineare Abbildung den Nullvektor auf sich selbst abbildet, ist der Nullvektor immer ein Fixvektor Wenn es neben dem Nullvektor noch weitereSwitch the x's and y's At this point you are dealing with the inverse;




Example 13 Define Function Y F X X 2 Complete The Table



What Does F 2 X Mean Is It F F X Or F X 2 Or F X Quora
So f (x) shows us the function is called " f ", and " x " goes in And we usually see what a function does with the input f (x) = x2 shows us that function " f " takes " x " and squares it Example with f (x) = x2 an input of 4 becomes an output of 16 In fact we can write f (4) = 16 The partial derivative of f with respect to x is fx(x, y, z) = lim h → 0f(x h, y, z) − f(x, y, z) h Similar definitions hold for fy(x, y, z) and fz(x, y, z) By taking partial derivatives of partial derivatives, we can find second partial derivatives of f with respect to z// other definition } X f () { X x;




Solving Trigonometric Equations Concept Methods




The Agony And Dx Dt The Meaning Of F X
2 Its function declaration of name f X f ();A market for the trading of currencies For example, one may buy dollars or sell pounds on a forex market Foreign exchange is one the largest and most liquid markets in the world Trading occurs overthecounter, and most of the major players are governments, banks, and speculators Forex markets are often used in hedging strategiesGraph f (x)=x Find the absolute value vertex In this case, the vertex for is Tap for more steps To find the coordinate of the vertex, set the inside of the absolute value equal to In this case, Replace the variable with in the expression The absolute value is the distance between a number and zero The distance between and is



What Is Calculus



Faculty Math Illinois Edu Hildebr 370 408discrete1 Pdf
I know this might be a stupid question but I can't seem to find the answer anywhere linearalgebra notation fieldtheory Share Cite Follow edited Sep 26 '15 at 301 Thomas Andrews 1 asked Sep 26 '15 at 2Show more Tbh thats about as good as most people would be able to do and i didnt know that f' (x) was dy/dx 0^ ^ function return type function f () takes no arguments and returns a X class object for example its definition can be like class X { int i;



1



F X Graph
Answered 2 years ago Upvoted by Quora User , master degree Mathematics (24) Author has 34K answers and 26M answer views f ( x) = x Function is giving the absolute value of x whether x is positive or negative See the y axis of graph which is f ( x) against x, as x axisDefinition Unter einer Stammfunktion einer reellen Funktion versteht man eine differenzierbare Funktion , deren Ableitungsfunktion ′ mit übereinstimmt Ist also auf einem Intervall definiert, so muss auf definiert und differenzierbar sein, und es muss für jede Zahl aus gelten ′ = () Existenz und Eindeutigkeit Jede auf einem Intervall stetige Funktion , → besitzt eine StammfunktionWhen we first got introduced a function composition we looked at of actually evaluating functions at a point or compositions of functions at a point what I want to do in this video is come up with expressions that define a function composition so for example I want to figure out what is f of G of X f of G of X and I encourage you to pause the video and try to think about it on your own well G



Solution Find The Range Of F X X 2 2x 1 Determine The Values Of X In The Domain Of 39 F 39 For Which F X 2 2 Means Squared




2 5 1 Explain The Meaning Of Lim F X 10 Choose The Chegg Com
X the inputs, factors or whatever is necessary to get the outcome (there can be more than one possible x) F the function or process that will take the inputs and make them into the desired outcome;Don't embarrass yourself by pronouncing (or thinking of) " f ( x ) " as being " f times x ", and never try to "multiply" the function name with its parenthesised inputIt is a different way of writing "y" in equations, but it's much more useful!



Http Maths Dur Ac Uk Dma0wjz B1 Anlec1 Pdf




For Which Of The Following Functions F Is F X F 1 X For All X Gmat Tutor In Nyc Online
Explanation Let f (x) = √1 2x Then the derivative at x = a is defined as the following limit f '(a) = lim h→0 f (a h) −f (a) h = lim h→0 √1 2(a h) − √1 2a h = lim h→0 √1 2(a h) − √1 2a h ⋅ √1 2(a h) √1 2a √1 2(a h) √1 2a = lim h→0 √1 2(a h) − √1 2a h ⋅ √1 2(a h) √1 2a √1 2(a h) √1 2a



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki
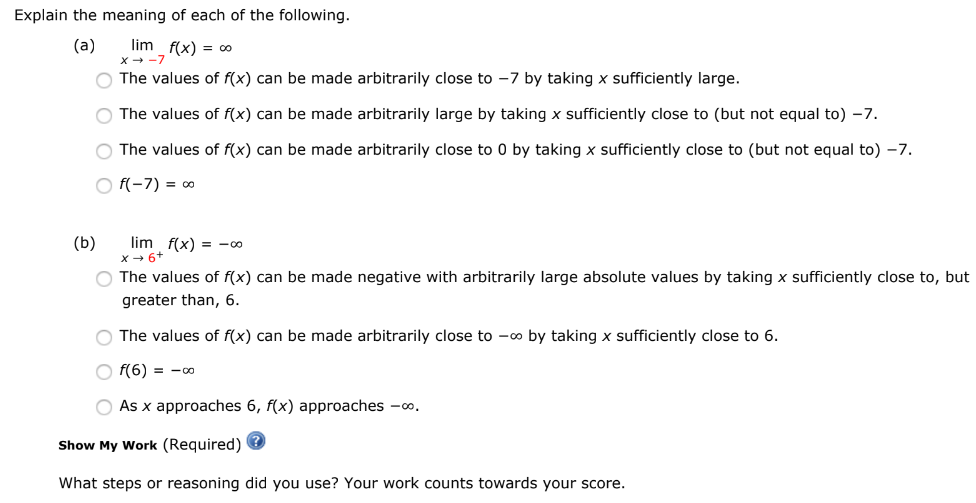



Answered Explain The Meaning Of Each Of The Bartleby




Inverse Functions Given 2 Functions F X G X If F G X X And G F X X Then F X G X Are Inverses Of Each Other Symbols F 1 X Means F Ppt Video Online Download




Function Mathematics Wikipedia




A Toy Illustration Of The Meaning Of Highprobability Safety Guarantees Download Scientific Diagram



Www Jstor Org Stable




Example 15 F X 1 X What Is The Domain And Range Examples




The Meaning Of The Mixed Partial Derivative F Sub Xy Sub



1




Meaning Of Phi In Spivak S Proof Of Inverse Function Theorem Mathematics Stack Exchange



Derivative Of E X Wyzant Lessons
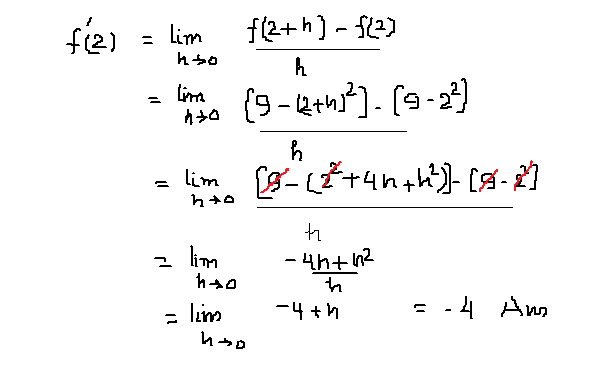



How Do You Find F 2 Using The Limit Definition Given F X 9 X 2 Socratic




Derivative Of F X 1 X Using The Limit Definition Youtube



Http Www Staff City Ac Uk O Castro Alvaredo Teaching Notes2 Pdf



What Is The Difference Between Y F X And Y F X Quora




Composition Of Functions Definition Examples Video Lesson Transcript Study Com



Http Aubg Edu Documents 248




B Value Definition Explanation Video Lesson Transcript Study Com



Calculus Limit Function Take The Limit As X Approaches




Using Function Notation What Is F X Youtube




Function Mathematics Wikipedia



Www Jstor Org Stable




What Is The Difference Between Y F X And Y F X Quora



1 1 Functions And Their Graphs




Answered A Use The Definition Of F To Show Bartleby




By Dr Julia Arnold The Algebra Of Functions What Does It Mean To Add Two Functions If F X 2x 3 And G X 4x 2 What Would F G X Be




How Do You Find F X If You Have A Value For X Virtual Nerd




7 1 What Does Fx Mean Youtube




How Do You Use The Limit Definition To Find The Derivative Of F X X 3 X 2 2x Socratic
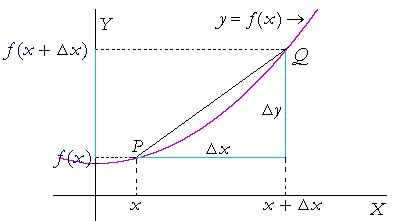



The Meaning Of The Derivative An Approach To Calculus




Composite Function Definition Examples Video Lesson Transcript Study Com




Inverse Functions Definition A Function Is A Set Of Ordered Pairs With No Two First Elements Alike F X X Y 3 2 1 4 7 6 9 12 Ppt Download



Graphs




The Domain Of Definition Of The Function F X Log X Is R B Oo 0 C 0 Oo D R 0




Definition Of The Derivative Youtube



Increasing And Decreasing Functions



What Is Calculus
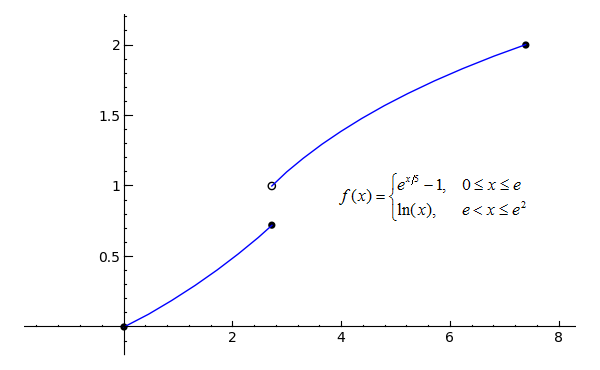



Sage Calculus Tutorial Continuity




What Is A Derivative Visual Explanation With Color Coded Examples And Graphs A Derivative Is Simply




Domain Range And Codomain




What Does F X Mean Youtube




Composite Functions And Inverse Functions Ppt Video Online Download




The Definition Of The Derivative Wolfram Demonstrations Project
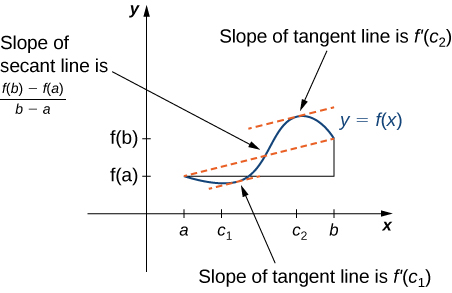



4 4 The Mean Value Theorem Calculus Volume 1



2
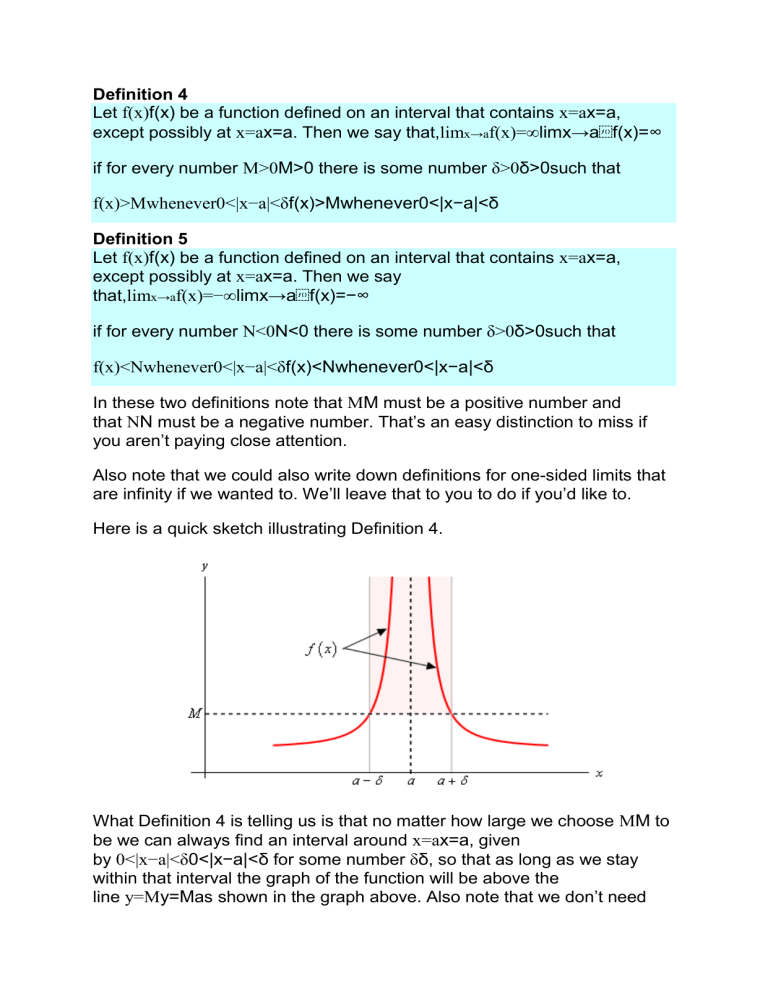



Definition 4




6 7 Notes Inverse Functions Notice How The X Y Values Are Reversed For The Original Function And The Reflected Functions Ppt Download



Domain And Range Of A Function



Calc 1 F X 0 If X 0 What Does This Mean Physics Forums
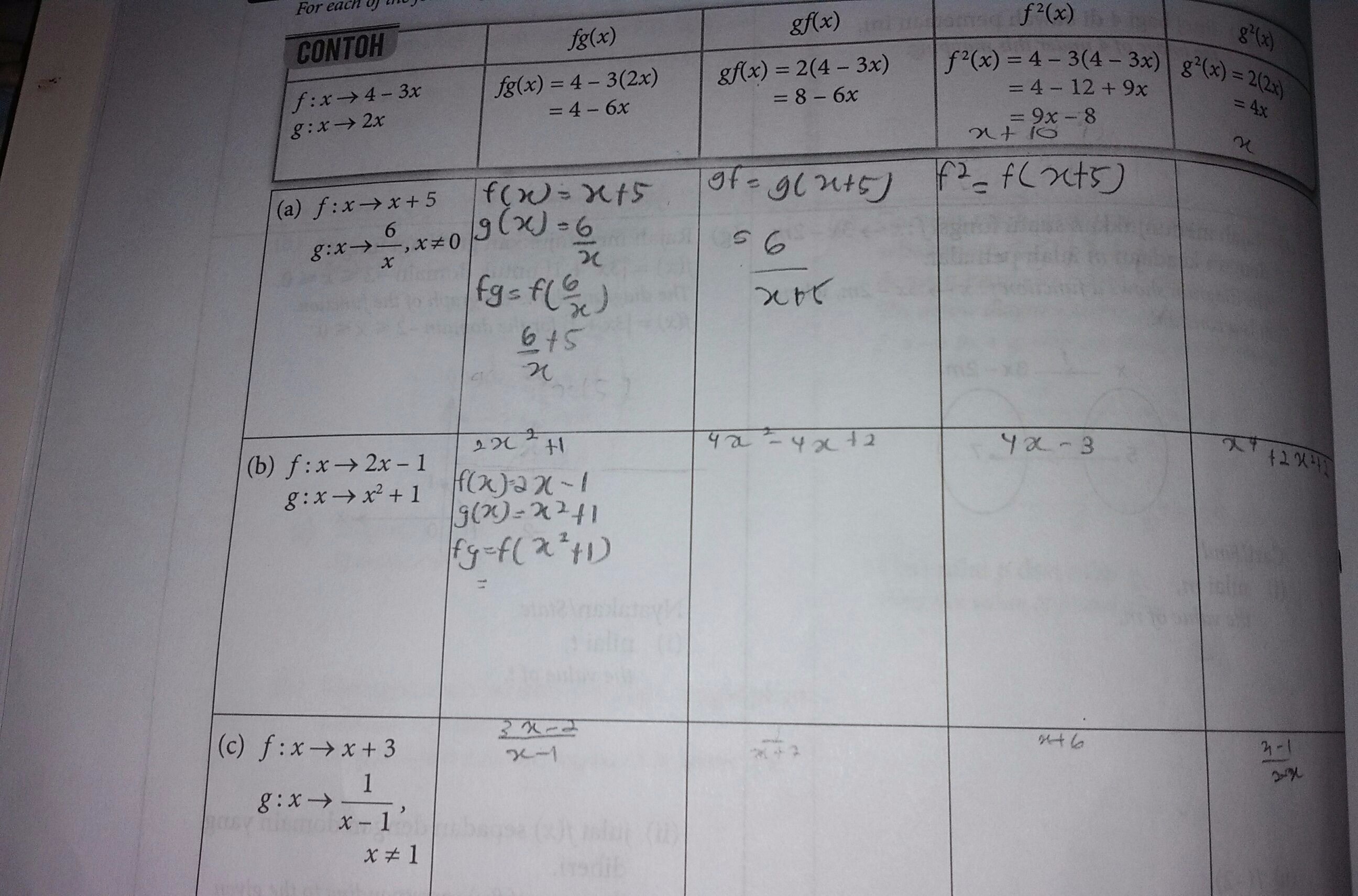



How To Solve Fg X Gf X F X G X For All Function In The Table Below Can Ask Manytutors



Faculty Math Illinois Edu Aydin Math2 Lecturenotes M2 Sec1 4 Pdf
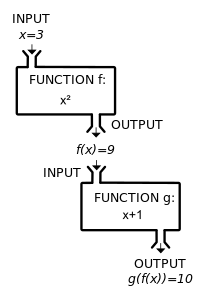



Function Mathematics Wikipedia



Probability Density Function



View Question Evaluate F X At K



Inverse Functions
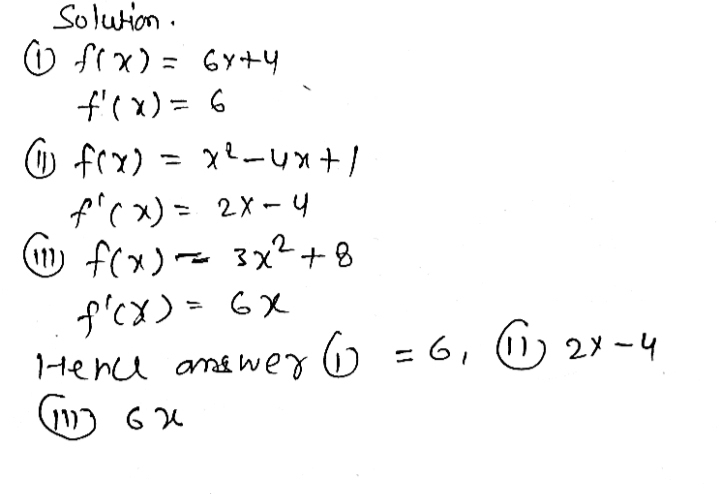



Find F X Using The Definition Of The Derivative W Gauthmath




Meaning Of Phi In Spivak S Proof Of Inverse Function Theorem Mathematics Stack Exchange



What Does F X X Mean Quora
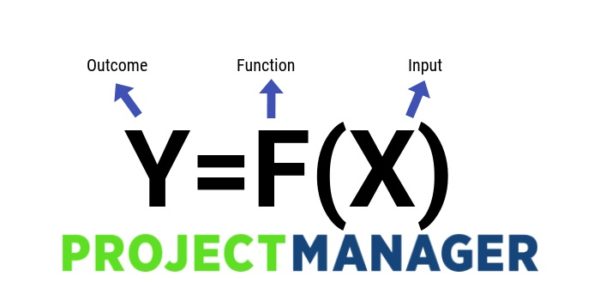



What S Does Y F X Mean How To Use This Powerful Six Sigma Formula
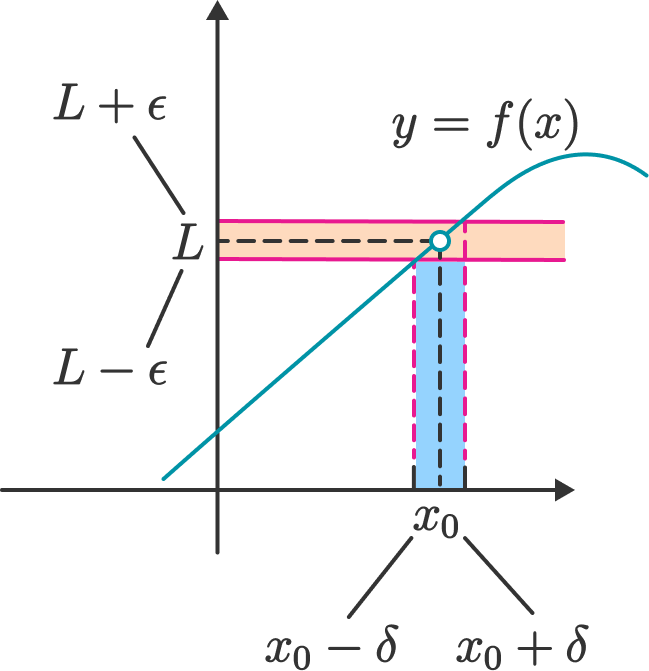



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki
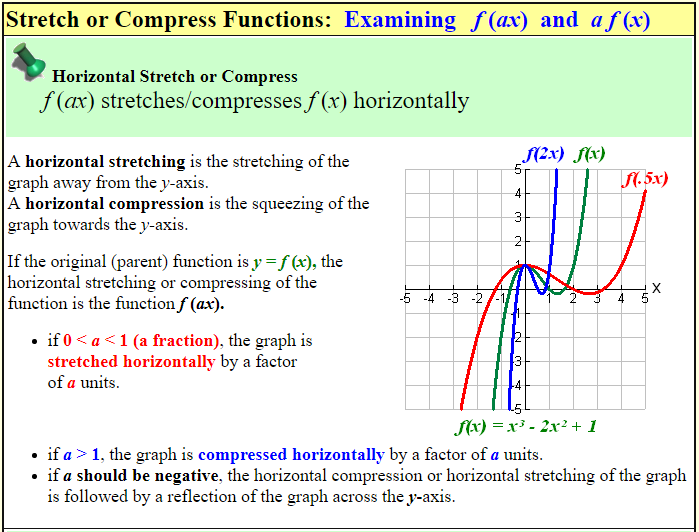



Shifting And Stretching Graphs The Math Doctors




Meaning Of The Notation Mathcal F X F X Mathematics Stack Exchange
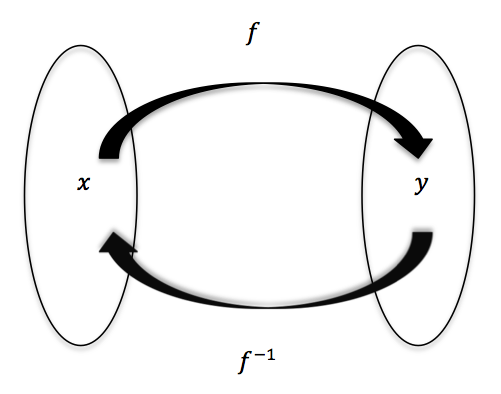



Functions And Their Inverses Worked Examples



Math Scene Derivatives Lesson 2 Differentiating Polynomials
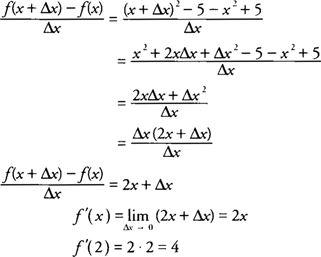



Definition



Surfaces As Graphs Of Functions Math Insight



The Epsilon Delta Definition Of A Limit




Domain Definition Examples Cuemath



Inflection Points




Using The Factor Theorem In Finding The Factors Of Polynomials With Examples Owlcation



No comments:
Post a Comment