In this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig idIf f(2tanx/(1 tan2x)) = 1/2(1 cos2x)(sec2x 2tanx) then find f(x) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesUsiong sec 2θ−tan 2θ=1⇒(2x) 2−( x2 ) 2=1, substitute the given values in terms of x⇒4x 2− x 24 =1⇒4(x 2− x 21 )=1⇒x 2− x 21 = 41

Integration Calculus Notes
Int tan 2x sec 2x / 1 tan 6x dx
Int tan 2x sec 2x / 1 tan 6x dx-Prove that cot x tan 2x1 =sec 2x Trigonometry How do you verify the equation is an identity?Integral of tan (2x)sec^2 (2x) \square!




Sec 2 2x 1 Tan2x Youtube
(x) 1 = sec²Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes{eq}\sec^2 x 1 = \tan^2x {/eq} (We multiply the expressions on the left using FOIL) {eq}1\tan^2 x 1 = \tan^2x {/eq} (We use the identity {eq}1tan^2(x)=sec^2(x) {/eq} {eq}\tan^2 x = \tan^2x
Solution for tan^2xsec^2x=1 equation Simplifying 1tan 2 x sec 2 x = 1 Solving 1an 2 tx c 2 esx = 1 Solving for variable 'a' Move all terms containing a to the left, all other terms to the rightA (cosxsinx)^2=12cosx sinx B1cos^2x/sin^2=1 Ctan^2x=sec^2xsin^2xcos^2x D (tanxcotx)^2=csc^2xsec^2x;X = 0, and x = pi, and x
Trigonometric Simplification Calculator \square!Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreAnswer (1 of 10) \int \frac{1\tan^2x}{1\tan^2x} \,dx \int \frac{1\tan^2x}{\sec^2x} \,dx \int \frac{1\tan^2x}{\frac{1}{\cos^2x}} \,dx \int \cos^2x(1\tan^2x) \,dx




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




Answered Find The Indefinite Integral Sec 2x Bartleby
Tan(2x) in terms of tan(x)orwrite cos(2x) in terms of tan(x)Get stepbystep solutions from expert tutors as fast as 1530 minutesProve tan^2(x) (1cot^2x) = sec^2x Prove tan^{2}(x) (1cot^{2}x) = sec^{2}x ar Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions ) If you've ever taken a ferris wheel ride then you know about periodic motion, you go up and down over and over




Solved 12 Evaluate The Integral Tan 2x 1 Sec 2x 1 Dx Chegg Com




If F 2tanx 1 Tan 2 X Cos2x 1 Sec 2 2tanx 2 Then F 4 I 1 Ii 3 Iii 0 Iv 5
Integral tan^2(x)sec(x)powers of secant and tangent Integral tan^2(x)sec(x)powers of secant and tangentAnswer (1 of 2) I = \displaystyle \int \dfrac{\tan x \cdot \sec^2 x \cdot dx}{1 \tan^2 x} \text{Let } t = \tan x\implies dt = \sec^2 x \cdot dx \therefore ITan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx Math Prove the identity sec^4x tan^4x = 12tan^2x
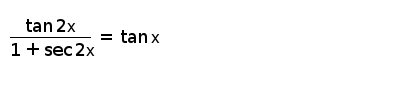



Tan 2x 1 Sec 2x Tan X




4 Tan 2x 2 Sec 2x 1 0 X In 0
Integration of sec^2x/1tan x (Solution)Integration of sec^2x/1tan x (Solution) dx this video teaches us how to Integration of sec^2x/1tan x (Solution) d\sec(2x^{1}1)\tan(2x^{1}1)\frac{\mathrm{d}}{\mathrm{d}x}(2x^{1}1) The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0Sec 22x=1−tan2x 1tan 22x=1−tan2x tan 22xtan2x=0 tan2x(tan2x1)=0 tan2x=0 or tan2x1=0 Now, tan2x=0 tan2x=tan0 2x=nπ0,n∈Z x= 2nπ




0 21 Solve By Inversion Method Y 1 0 22 Find The General Solution Of




Solved Evaluate Integral Tan 6 2x Sec 4 2x Dx If We Chegg Com
Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2TRIGONOMETRY LAWS AND IDENTITIES QUOTIENT IDENTITIES tan(x)= sin(x) cos(x) cot(x)= cos(x) sin(x) RECIPROCAL IDENTITIES csc(x)= 1 sin(x) sec(x)= 1 cos(x) cot(x)= 1 tan(x) sin(x)= 1 csc(x)Which of the following is not an identity?
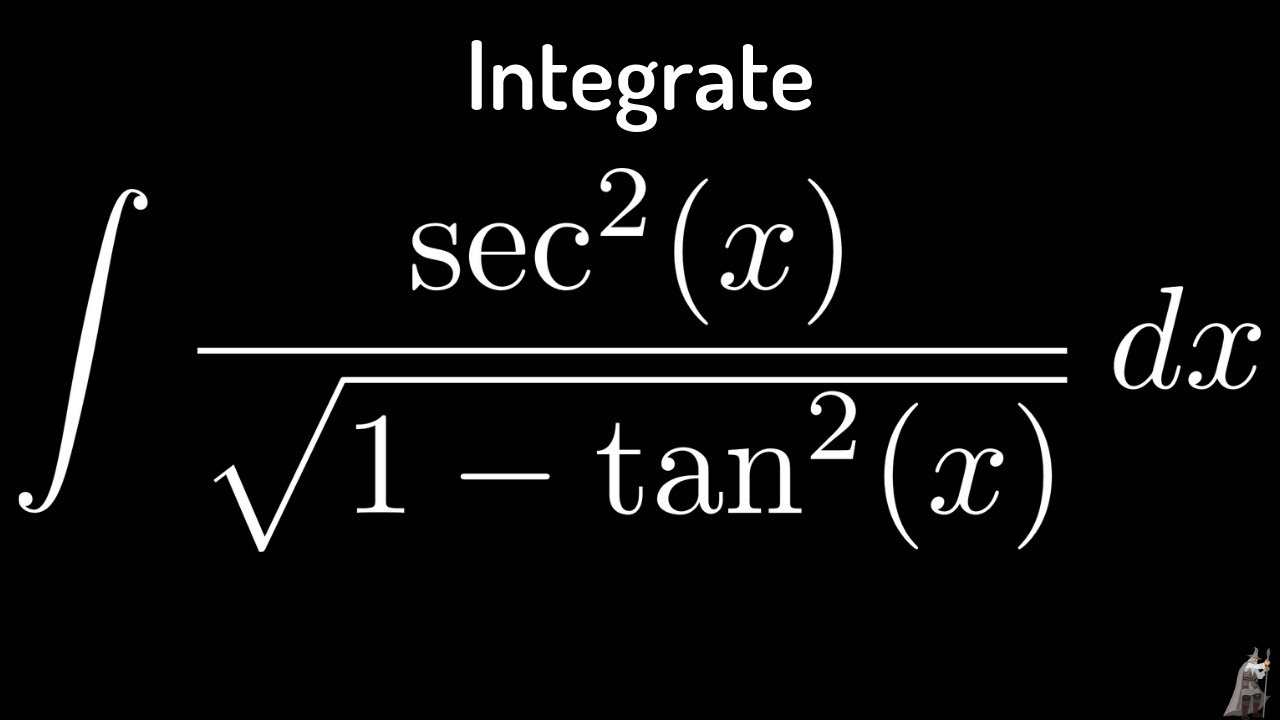



Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube




Match The Corresponding Trigonometric Expressions Gauthmath
A follow up proof to accompany sin^2 cos^2 =1 Another identity that is used quite a bit, especially in calculus involving trigonometric functionsAnswer (1 of 42) All these good answers are algebraic proof If we want to visualize this whole thing geometrically(And if computer has to draw the picture and proof without human intervention) then GeometrifyingTrigonometry which is a part of Geometric Automata WeiEx 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 ta



Solve Sec 22x 1 Tan2x Sarthaks Econnect Largest Online Education Community




Tan 2x Sec 2x 1 True Or False For All Values Of X Wyzant Ask An Expert
Click here👆to get an answer to your question ️ If sec x sec^ 2x = 1 then the value of tan^ 8 tan^ 4 2tan^ 2x 1 will be equal toAsked by jjroberts Mathematics Answered Out Which of the following is not an identity?We get (tan(x))2 1 = (sec(x))2 1 = (sec(x))2 (tan(x))2 Now, we will see if 1 = (sec(x))2 (tan(x))2and 1 = (sec(x))2 (tan(x))2 can both be true We can do this by assuming that they are both true, and then add the equations to get 2 = 2(sec(x))2 1=(sec(x))2




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
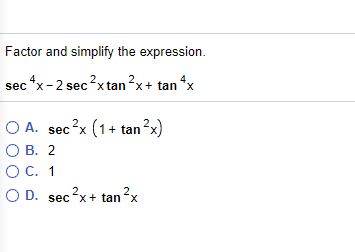



Solved Factor And Simplify The Expression Sec 4 X 2 Chegg Com
See the proof below We need tanx=sinx/cosx sin^2xcos^2x=1 secx=1/cosx Therefore, LHS=tan^2x1 =sin^2x/cos^2x1 =(sin^2xcos^2x)/cos^2x =1/cos^2x =sec^2x =RHS QED Trigonometry ScienceRaise sec(2x) sec ( 2 x) to the power of 1 1 Use the power rule aman = amn a m a n = a m n to combine exponents Add 2 2 and 1 1 Since 2 2 is constant with respect to x x, the derivative of 2x 2 x with respect to x x is 2 d dx x 2 d d x x Multiply 2 2 by −1 1Answer (1 of 4) In Trigonemetry Laws and Identities, there are some rule that we will use to prove 1 / sec²



1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib




Integrate Tan 3 2x Sec2x Brainly In
Next, y dash = sec^2xtan^2x tanx/sec x = 1 tan x/sec x Derivative of tan x^ cot x Let y equals tan x to the power cot x The first method, a to the power b equals to e to the power b log a So, y equals to e to the power cot x log tan x Differentiate with respect to x, dy upon dx equals to e to the power cot x log tan x into differentiateCot (x) = cot (x) sin ^2 (x) cos ^2 (x) = 1 tan ^2 (x) 1 = sec ^2 (x) cot ^2 (x) 1 = csc ^2 (x) sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x)Prove tan^{2}(x) (1cot^{2}x) = sec^{2}x en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identity




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Solution Integral Of 3 Sec 2x 1 Tan 2x 1 Studypool
Tan^2 x=sec^2 x1=(sec x1)(sec x 1) rArr tan^2 x/(sec x1)=sec x1, or, =(1cos x)/cos x,Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!(x) = 1 * tan (x) = sin (x) / cos (x) We will prove from the Left Hand Side We know that sec²




Sec 2 2x 1 Tan2x Youtube




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
(x) 1, so 1 /Evaluate \(\int\frac{tanx\,sec^2x}{(1tan^2x)}dx\) ∫tanx sec2x/(1 tan2x)dxStarts from RHS to LHS




Question 34 Ssssd Maths Integrals Meritnation Com
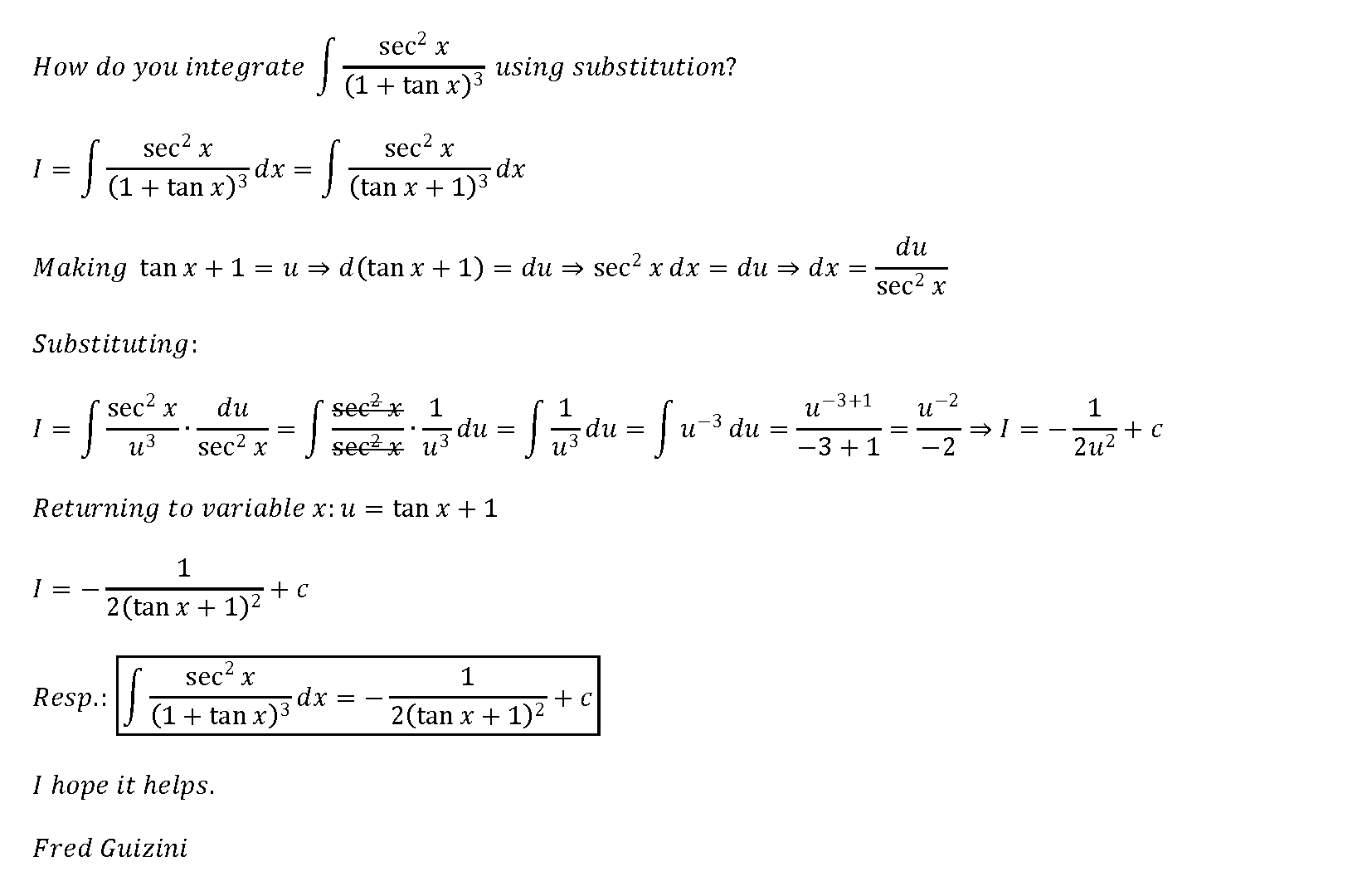



How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `sec^(2)2x=1tan2x`Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan) But the book's answer is the cosecant of beta Math What is a simplified form of the expression sec^2x1/(sinx)(secx)?Calculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x)




Get Answer 1 Tan2x Sec2x Dx Sin2x 2 C Tan 2 X 2 C 2sin X Cos X Transtutors




3 Sec 2x1 Cos2 X Tan 2x Tantx E Sus S Always The An 0 Om Sec Meme On Me Me
Integrating Al and Bl wrt x, We have A — sin 2x— log ( sec 2x tan 2N )CI B — cos2x Hence complete solution is y— cos 2x c2 sin2x — cos 2x log (sec 2x tan 2x) Ans EM52 Q14 Solve d2y dy 3 v2 dv BTech (11 serm) Hence the given equation is not exact therefore to use an integration factor here to change the given' h into0, (3pi)/4, pi, (7pi)/4, 2pi There are 2 variables sin x and cos x General Method we must transform the trig equation into a product of 2 simple trig equations 1/(cos^2 x) sin x/(cos x) = 1 1 sin xcos x = cos^2 x (1 cos^2 x) sin xcos x = 0 sin^2 x sin xcos x = 0 sin x(sin x cos x) = 0 Now, we solve the two simple trig equations a sin x = 0 >A (cosxsinx)^2=12cosx sinx B1cos^2x/sin^2=1 Ctan^2x=sec^2xsin^2xcos^2x D (tanxcotx)^2=csc^2x




Toppr Ask Question




Analytic Trig Ppt Video Online Download
Solution for Sec^2x=1tan^2x equation Simplifying Sec 2 x = 1 tan 2 x Solving c 2 exS = 1 an 2 tx Solving for variable 'c' Move all terms containing c to the left, all other terms to the right Divide each side by 'exS' c 2 = e1 x1 S1 ae1 n 2 tS1 Simplifying c 2 = e1 x1 S1 ae1 n 2 tS1 Reorder the terms c 2 = ae1 n 2 tS1 e1 x1 S1 Reorder the terms 1ae1 n 2 tS1Separate fractions Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Convert from cos(x) sin(x) cos ( x) sin ( x) to cot(x) cot ( x) Divide sec2(x) sec 2 ( x) by 1 1 Rewrite sec(x) sec (Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graph




Dx 2 Va X Exercise 7 C Differentiate The Following Functions With Respect To X 1




Sec 2x1 Cos2 X Tan 2x Tantx 3 Esus Is Always The Ans イais 1 0 Studentlifeproblems If You Are A Student Follow Tumblr Meme On Me Me
Answer (1 of 2) sec^2(2x) = 1 tan (2x) 1 tan^2(2x) = 1 tan(2x) tan^2 (2x) tan (2x) = 0 tan(2x) tan (2x) 1 = 0 either tan (2x) = 0 = tan (0°) 2x = npiRewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)\\int \tan^{2}x\sec{x} \, dx\ >




Trig Identities Ppt Download
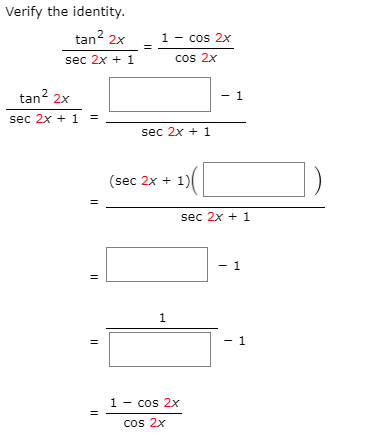



Solved Verify The Identity Tan 2x 1 Cos 2x Cos 2x Sec 2x Chegg Com
Answer (1 of 4) Define fR \to R by f(x)=tan(2x)2x Then f'(x)=2sec(2x)2>=0 on (\pi/2,\pi/2) which means f is increasing on (\pi/2,\pi/2) Since tan(2x) ranges from (\infty,\infty) within the interval, we can find a solution for f(x)=0, which, within this range, is 0 Then, note that withWell, if we divide (cos(x))2 on both sides;If sec θ = x (1/4x), prove that sec θ tan θ = 2x or 1/2x



Pythagorean Identities
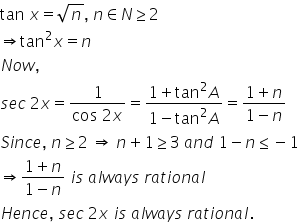



Tanx Root N Where N Belongs To N2 Then Sec 2x Is Always Rational Irrational Positive Or Negative Mathematics Topperlearning Com Id3lcoyy




Identidades Trigonometricas Pdf




Sec 2 2x 1 Tan2x Youtube




Integration Tan Sec2x 1 Tan2x Dx Mathematics Topperlearning Com Fod22d




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Homeworklib




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Integration Calculus Notes



Prove That Tan2x 1 Sec2x Tanx Sarthaks Econnect Largest Online Education Community




2 Tan X 1 Tan 2 X Wyzant Ask An Expert Liana Charlne Ebooks En Ligne




Sec 1 1 Tan 2x 1 Tan 2 X




Solved Verify That The Equation Is An Identity 1 Tan X Chegg Com




Integrate Sec 2x Method 2




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



What Is The Integral Of Tanx Sec 2x 1 Tan 2x Quora




Tan2x ただの悪魔の画像




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Sec 2x 1 Tan 2x Brainly In




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit




いろいろ Tan2x 1sec2x ただの悪魔の画像




Solution 3 Sec Maths Studypool



1 Tan 2x A Cos 2x B Sin 2x C Cot 2x D Sec 2x Gauthmath



Evaluate Sec X Tan X 1 Sec 2 X Dx X 0 P 3 Sarthaks Econnect Largest Online Education Community




いろいろ Tan2x 1sec2x ただの悪魔の画像




Tan 2x 1 Sec 2x Tan X Sin X Cos X 2 1 Sin 2x Youtube




For N In N Let F N X Tan X 2 1 Sec X 1 Sec 2x 1 Sec 4x 1 Sec 2 N X The Lim Xto0 F N X 2x Is Equal To




Proof Tan 2 1 Sec 2 Youtube
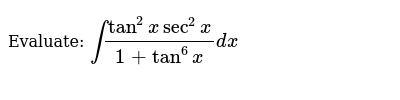



Evaluate Int Tan 2xsec 2x 1 Tan 6x Dx




Sec 8x 1 Sec 4x 1 Tan 8x Tan 2x Maths Trigonometric Functions Meritnation Com




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Tan2x Sec2x ただの悪魔の画像




Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange




Tan2x Sec2x ただの悪魔の画像
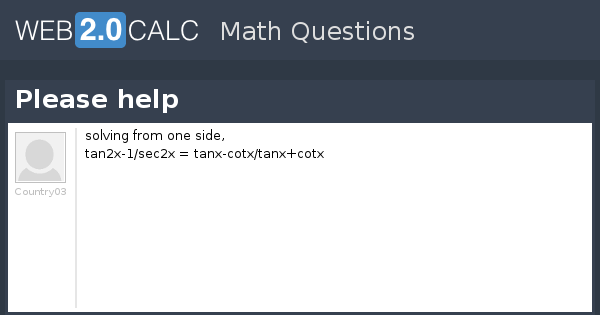



View Question Please Help




Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In



For N Belong To N Fn X Tan X 2 1 Sec X 1 Sec 2x 1 Sec4x 1 Sec 2 N X Then Lim Fn X 2x Is Equal To
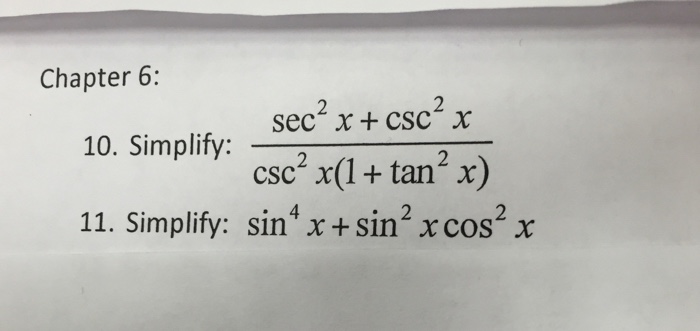



Solved 10 Simplify Sec 2x Csc 2x Csc 2x 1 Tan 2x 11 Chegg Com
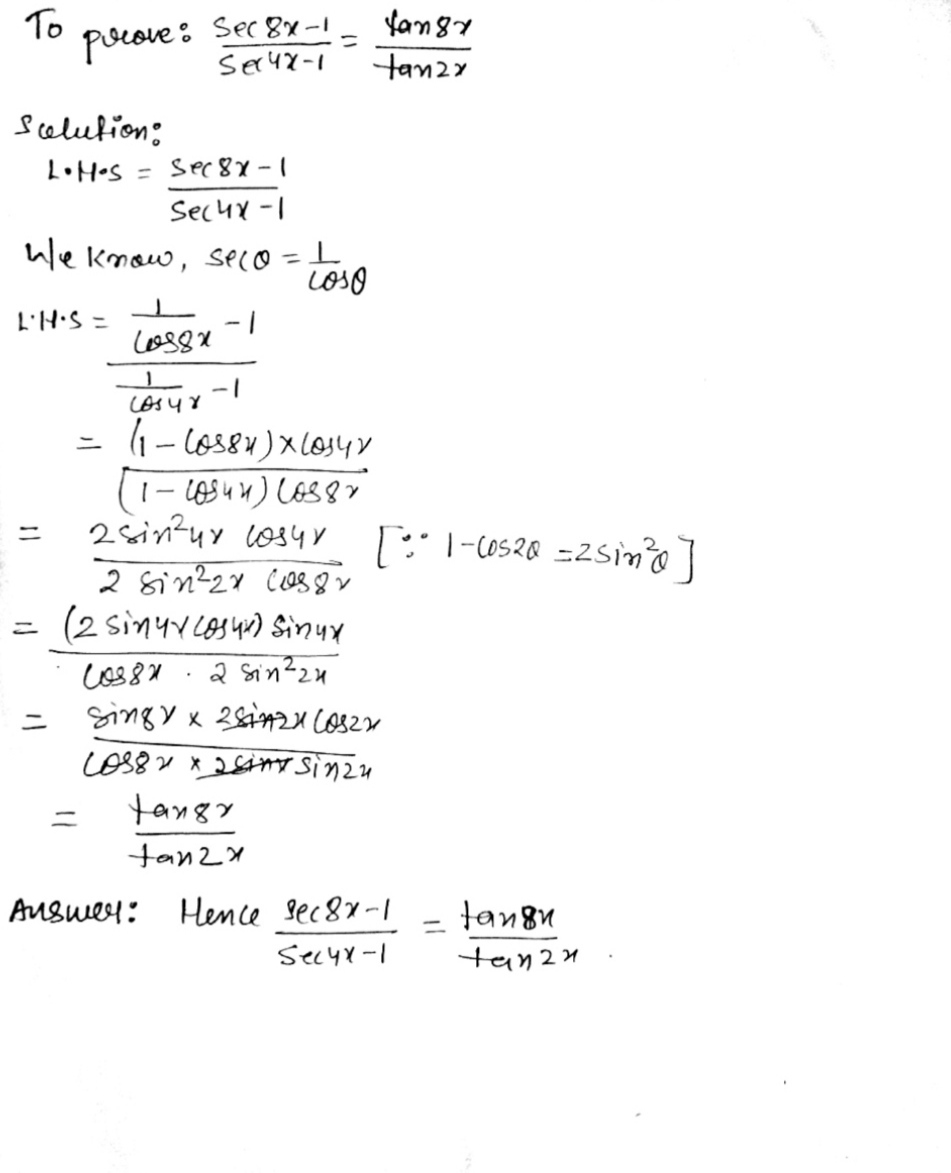



Prove That Frac Mathit Sec 8x 1 Mathit Sec 4x 1 Frac Tan 8x Tan 2x Snapsolve
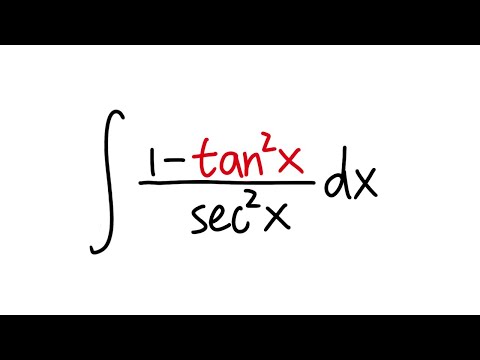



Q45 Integral Of 1 Tan 2x Sec 2x Youtube




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3




Integral 1 Tan 2 X Sec 2 X Youtube
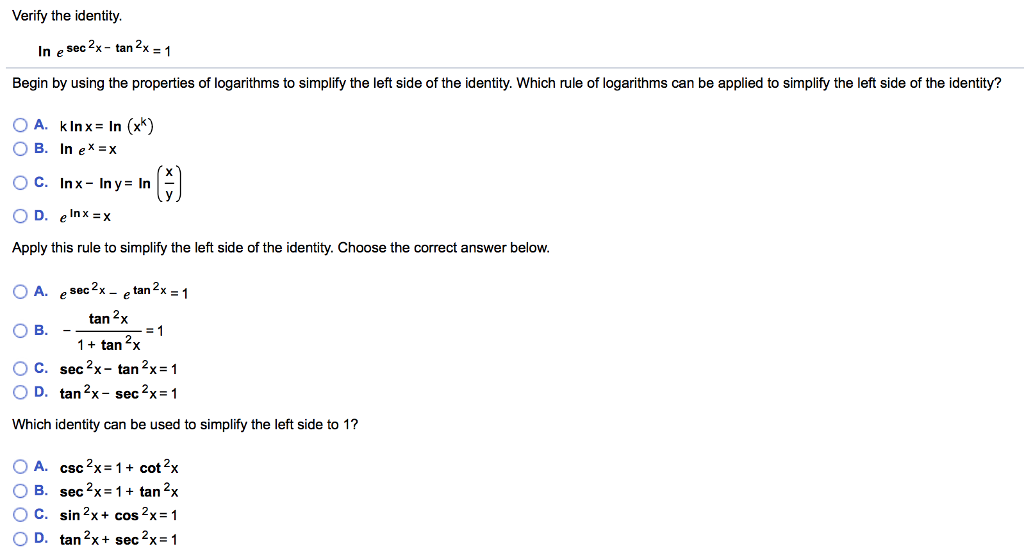



Solved Verify The Identity In Esec 2x Tan 2x 1 Begin By Chegg Com



How To Integrate Math Dfrac X Sec 2x 1 Tan X Math Quora
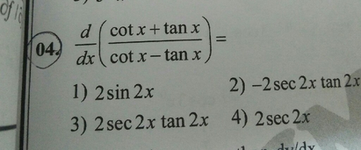



D Cotx Tanx Dx Cot X Tan X 1 2sin 2x 04 2 2 Sec 2x Tan 2 Scholr




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube




Tan2x Sec2x ただの悪魔の画像




7 Techniques Of Integration Techniques Of Integration 7



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction



Differentiate The Sec 1 1 Tan 2x 1 Tan 2x W R T X Sarthaks Econnect Largest Online Education Community



3



Solved Solve The Following Sec Order Non Homo Equation There Is Answer Provided Course Hero



If Tan X T Then Tan 2x Sec 2x Is Equal To A 1 T 1 T Sarthaks Econnect Largest Online Education Community



1




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com




Integral Sec 3 2x Tan 2x Dx



Solution Verify The Identity By Showing That The Left Equals Right Sec 2x 1 Tan 2 Sec2x Do I Use 1 Cos 2x 1 Tan 2x Or Do I Use 1 Tan 2x 1 Tan 2x Either Way I Do Not Know Where To Go Fro



Is There A Geometrical Method To Prove X Frac Sin X Tan X 2 Mathematics Stack Exchange
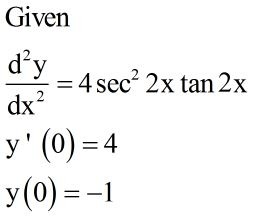



Answered D Y 4 Sec 2x Tan 2x Y 0 4 Y Bartleby




How Many Can You Derive From First Principles Ppt Download




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




3 Sec 2x1 Cos 2x Tan 2x Tan X Esus Is Always The Anse Ja Irl Meme On Me Me




3 Sec 2x1 Cos2 X Tan 2x Tantx E Sus S Always The An 0 Om Sec Meme On Me Me




Mathematics Question Of The Day With Solution Facebook
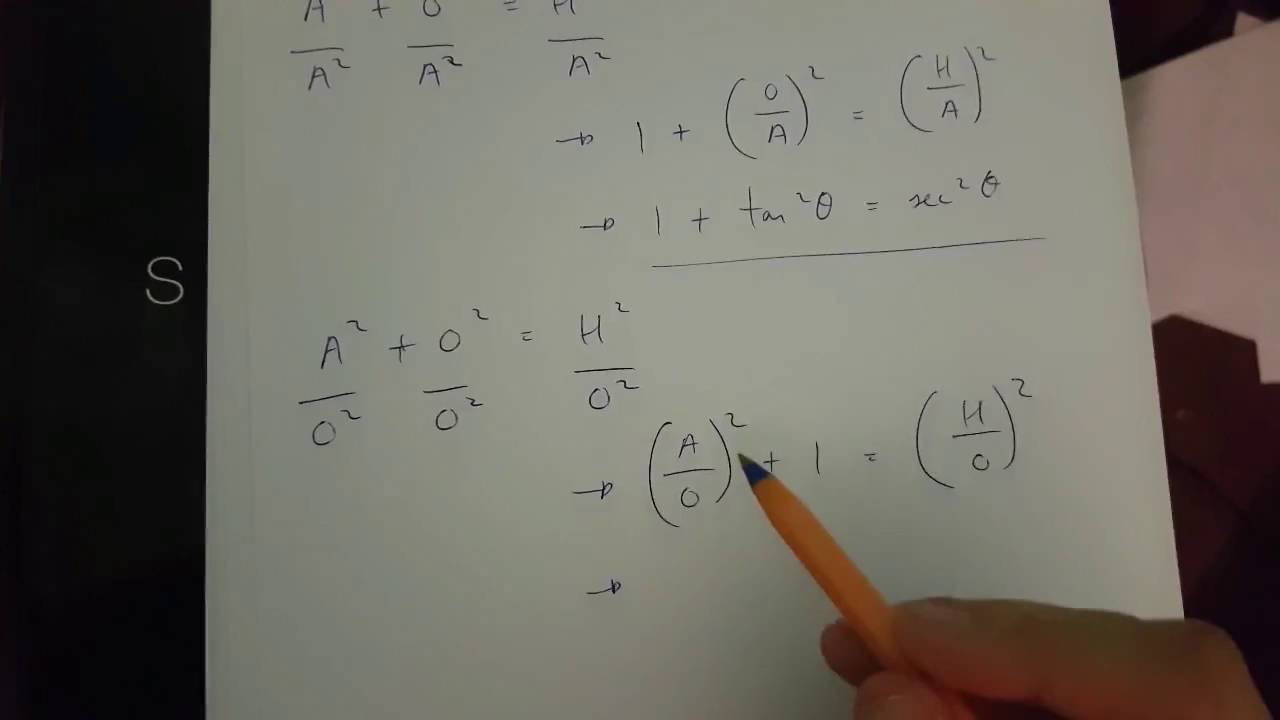



How Do You Prove Tan 2x Secx 1 1 Secx Socratic



1




7 Techniques Of Integration Techniques Of Integration 7
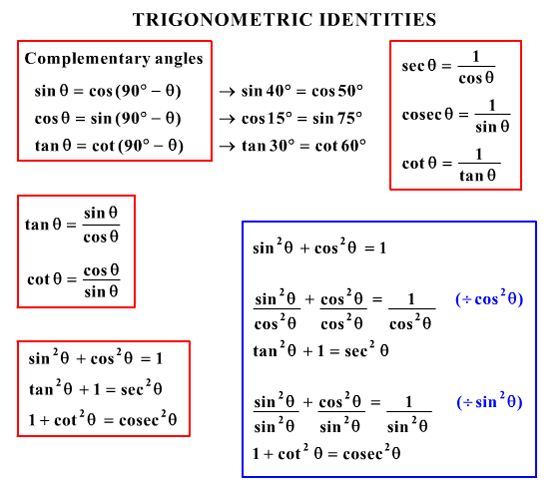



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic




I M Seriously Confused About This Trigonometry Problem Askmath




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



How Do We Prove That Tan2x 1 Sec2x Tanx Quora




いろいろ Tan2x 1sec2x ただの悪魔の画像



No comments:
Post a Comment